How Interconnects Work: Anatomy of Crosstalk
Models for understanding sources, quantification and mitigation of crosstalk.
by Yuriy Shlepnev
Crosstalk in PCB and packaging interconnects is arguably one of the most complicated phenomena that may cause signal degradation. It is caused by unwanted coupling between signal links and between signal links and power distribution systems. The effect is deterministic, but very difficult to predict in many cases – too many variables and uncertainties. Crosstalk effects can be treated statistically as a deterministic jitter with a bounded distribution, but the distribution is usually not known and just guessed.
A direct analysis of a worst-case crosstalk scenario may lead to a system overdesign. Neglecting it in design may cause a system failure that is difficult to find and fix later in a design process. On top of that, distortions caused by crosstalk cannot be corrected by signal conditioning techniques at the receiver side. Thus, it is very important to understand the sources of crosstalk, how to quantify it and how to mitigate it efficiently. This is the first part of the paper with an overview of crosstalk sources and terminology – just a slice through the complicated phenomenon. The second part will describe and compare different ways to quantify, compute and measure crosstalk. This paper continues the “How Interconnects Work” series.1-4
Crosstalk in the Balance of Power
The best way to describe “what happens to a signal on the way to the receiver” is to use the balance of power, which can be written for a passive interconnect as follows4:
P_out = P_in – P_absorbed – P_reflected – P_leaked + P_coupled
This is applicable to both the time domain and the frequency domain over the bandwidth of a signal1. P_in is the power delivered by a transmitter to the interconnect (useful signal) and P_out is the power delivered to a receiver (degraded useful signal + noise). All other terms in the balance of power equation describe the signal distortion. The absorption and reflection terms (P_absorbed and P_reflected) were discussed in the previous papers of the “How Interconnects Work” series.2-4 This paper is about P_leaked and P_coupled or the crosstalk parameters:
P_leaked is power leaked into other coupled interconnects, into the common mode and possibly, into power distribution network (PDN is just another type of interconnect) and into free space (radiated) – that leak causes signal distortion and is a possible source of crosstalk in addition to being source of EMC/EMI.
P_coupled is power gained from the other coupled interconnects, common mode, PDN and free space – this is the crosstalk.
Crosstalk in general is just unwanted noise from the coupled structures (P_coupled) caused by unwanted signal leaks (P_leaked) that degrade the useful signal and may reduce the data transmission rate and even cause complete link failure.
Crosstalk Types
Unwanted coupling in PCB and packaging interconnects can be separated into local and distant couplings:
- Local coupling between closely spaced traces and vias:
- Coupling in closely routed signal traces – the most common source of crosstalk
- Common to differential mode interference and crosstalk due to modal transformations in differential pairs (caused by bends, asymmetry in routing, fiber weave effect)
- Local couplings through slots and cutouts in reference planes
- Local coupling between vias and between vias and traces due to proximity.
- Distant coupling through parallel planes and split planes (slots), and through surface dielectric layers and PCB enclosure (multipath propagation).
Local couplings can be accurately simulated in general and taken into account during pre- and post-layout signal integrity analysis. Coupling in parallel traces can cause not only crosstalk and interference (unwanted noise), but also additional losses due to signal energy leaks to adjacent links (suck outs) – this is P_leaked in the balance of power. Leak losses may be significant in traces routed on the surface of PCB (microstrips). They are usually negligible for traces routed between parallel planes (striplines), however.
The distant coupling may cause a system-level interference and requires complete PCB or package analysis. The distant system-level coupling is very difficult to model and predict with sufficient accuracy. It can, however, be avoided (no rouging over split planes) or easily reduced by enforcing the localization for each structure that may potentially be coupled to parallel planes (transmission planes), surface dielectric layers or to the enclosure. Such coupling occurs at locations of changes in reference conductors. Unlocalized vias are the major source of leaks and crosstalk that can be easily avoided with the use of more stitching vias closer to signal vias, for instance. The system-level interference must be avoided by use of only the structures that are predictably localized up to the target frequency (conditional localization).
Crosstalk Origin
PCB and packaging interconnects, such as striplines, microstrip lines and coplanar waveguides, are open waveguiding structures. This means that the signal energy propagates along the PCB and packaging traces mostly in dielectrics around the signal conductors. It can be illustrated with the peak power flow density (vector product of electric and magnetic field) for a typical PCB stripline interconnect shown in Figure 1. This is the peak power flow density (PFD) of a signal with 0.5V magnitude normalized to maximal value and expressed in dB as 10*log|P|.
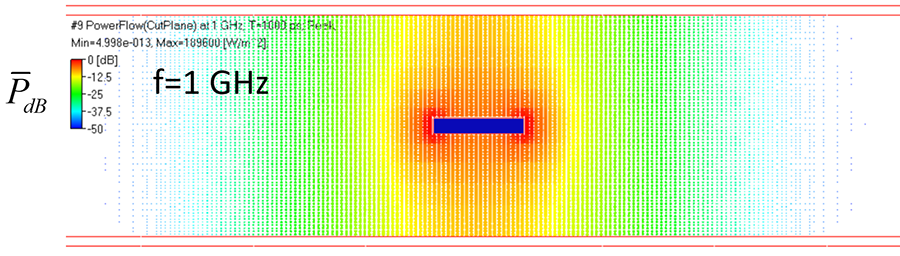
As you can see, there is no exact localization of the signal energy. The power flow density or signal energy concentrates near the strip edges and between the strip and planes. The red and yellow area is where most of the signal energy propagates. But it is also nonnegligible in in the green area of two to three strip widths in this case. Everything that gets into zone with green PFD (-25 to -30dB level, two to three widths of strip on both sides) becomes coupled, and that coupling may cause interference or crosstalk and signal leaks. In addition, the coupling changes the strip impedance. The image in Figure 1 is for the dominant strip line mode that has equipotential reference planes.
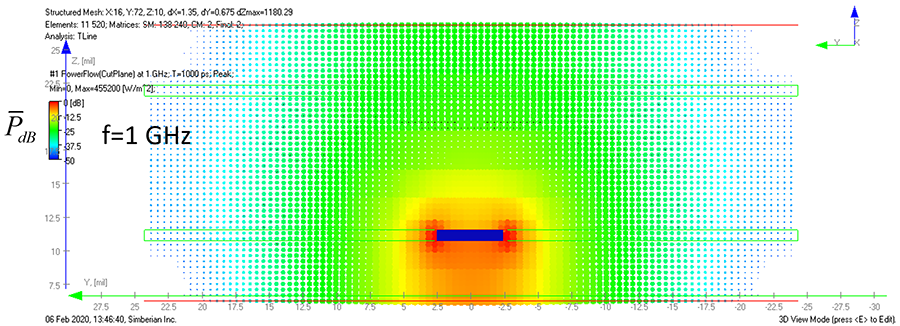
The signal energy spreading around a signal conductor is even worse in traces routed on a surface of PCB (microstrips) as we can see from Figure 2.

As we can see, the area of potential coupling is larger in the air as well as in the substrate – the trace can be effectively coupled to nearby traces as well as to any external objects in the area with green PFD (-25 to -30dB).
Similar or even worse extension of the coupling area can be observed in unsymmetrical strip lines as illustrated in Figure 3.
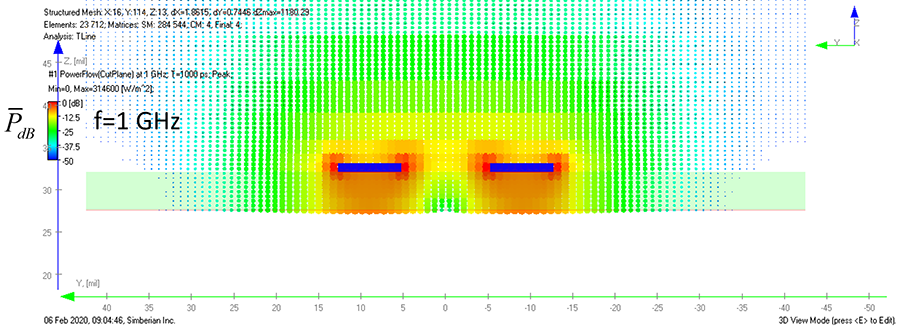
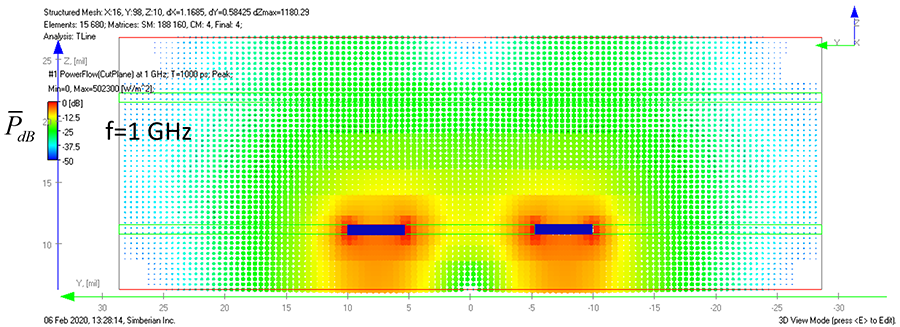
The differential mode in loosely coupled differential traces has signal energy spread similar to the single-ended case as illustrated by the peak power flow density for a typical differential microstrip in Figure 4. Peak PFD for a differential mode in a differential stripline with unsymmetrical reference planes is shown in Figure 5. As we can see, the distant reference planes may substantially increase the area where strips can be coupled even in the differential cases. The PFDs in Figures 4 and 5 are for the differential modes with excitation +0.5/-0.5V. The power of the differential mode flows around each trace in the same direction mostly along the traces.
The currents at microwave frequencies are not “flowing” and not “returning” anywhere – they are just a part of the wave propagation process and conductor energy absorption. The power flow density is the best way to visualize the physics of a signal propagation. The surface currents in the reference conductors can be used to evaluate possible coupling areas, yet it is not so intuitive and obvious as with the PFD.
In general, it is important to understand that a single trace is a two-conductor transmission line or waveguiding structure: the second conductor is always the reference plane (microstrip) or two planes (stripline). Differential traces are a three-conductor transmission line and the currents in the reference conductor are also spreading beyond the traces, similar to the single-ended cases. Reference conductors or planes in the signal energy propagation area are as important as the traces themselves. In a case of two reference planes, the equipotentiality of the planes along the signal propagation must be ensured with more stitching vias and even via fences, to avoid coupling to the dominant mode of the parallel plane structures; such coupling may occur at discontinuities such as vias and at dielectric inhomogeneities. Enforcement of the reference equipotentiality for coplanar transmission lines is even more complicated.
The bottom line is that the PCB and packaging interconnects are the open waveguiding structures with the signals propagating in space around the signal traces. Getting a signal with spectrum in microwave and millimeter-wave bandwidth from one component to another through an open waveguiding structure and without interaction with other signals is always a challenge.
Useful Crosstalk Terminology
Before proceeding with crosstalk modeling and quantification, let’s define some common terms.
- Stripline – model for traces routed on the internal layers of PCB/PKG with two reference planes and mostly homogeneous dielectric
- Microstrip line – model for traces routed on surface of PCB/PKG with one reference plane and inhomogeneous dielectric
- Coplanar line – model of traces with additional reference conductors in the same layer with the signal traces
- Aggressor is a transmitter (Tx) or a link with a signal that may cause interference in other links
- Victim is a receiver (Rx) or a link that may pick up unwanted interference caused by an aggressor link
- NEXT – near end crosstalk is interference observed at the link side that is closer to the aggressor link transmitter or signal source
- FEXT – far end crosstalk is interference observed at the link side opposite to the aggressor link transmitter or signal source.
There are many more terms for the crosstalk characterization. PSXT, MDXT, ICN, ICR and some others will be introduced and explained in the next section on crosstalk quantification.
Crosstalk in Parallel Traces
To illustrate interference of signals in parallel segments of microstrip line (surface trace), we will use two single-ended links routed at a distance equal to one trace width over 1.0″ distance. The characteristic impedance of each single trace is close to 50Ω. In the first case a signal propagates in the top trace from port p1 to port p3 as illustrated in Figure 6.
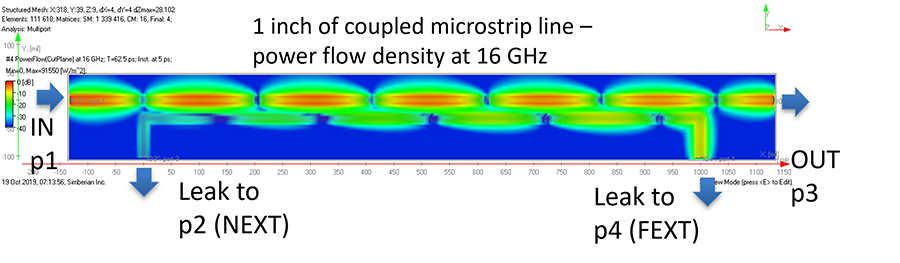
As we can see, the bottom link with ports p2 and p4 is literally in the “signal space” of the top trace. As the consequence, the bottom trace is coupled and “sucks out” some signal energy. Some useful signal power leaks into port p2 near the signal source (NEXT) and into port p4 on the side opposite to the signal source (FEXT). The leak is the result of the wave energy redistribution over the length of the coupled segment. How much energy is leaked and what are the consequences of that leak if there is a useful signal propagating in both links?
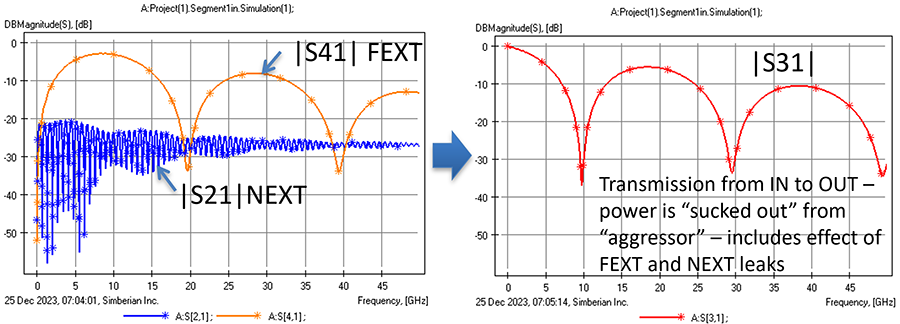
The most fundamental and convenient way to describe this energy redistribution phenomenon is with scattering parameters or S-parameters.5,6 It is very important to be familiar with the S-parameters. In fact, practically all other interconnect quality metrics including crosstalk quantification parameters are simply derived from the S-parameters. Magnitudes of the S-parameters describing the process of the energy redistribution for the structure from Figure 6 are shown in Figure 7.

Parameter S31 on the right graph of Figure 7 is the transmission of the useful signal from port p1 to port p3. Parameters S41 and S21 are the leaks and potential crosstalk parameters. The transmission|S31| is decreasing with the frequency, but with the slope that is much steeper than expected due to the material absorption losses.2 The reflection or return losses are very small in this case. The reason for this is a leak into port p4 that is described by S-parameter S41 on the left graph in Figure 7. The leak into port p2 is much smaller in this case. With a useful signal at port p4, parameter S41 becomes far end crosstalk, or FEXT. It is frequency-dependent, and the maxima and minima are defined by difference of propagation velocities of the even and odd modes in the coupled segment and by the segment length. There is no FEXT if this difference is zero or close to zero.
FEXT can be observed in any lossy multi-conductor transmission line in general, but it becomes substantial only in cases of transmission lines with inhomogeneous dielectrics – microstrip lines for instance. Striplines with dielectric layers with different properties also have observable and not-negligible FEXT. FEXT increases with the length of the coupled traces up to some level and then decreases, until it reaches minimum. Then minima and maxima repeat periodically with the frequency. In general, more energy from an aggressor link may leak into a victim link on links with longer coupling sections. The leak can interfere with the victim signal and degrade it. On the other hand, the leak also degrades the aggressor signal; it causes additional losses that can be comparable or even larger than the reflection and the material absorption losses. In fact, there might be conditions when almost all energy of the aggressor signal becomes FEXT. In the case above, almost complete suck out happens around 50GHz. For the same traces coupled over a longer 5″ segment, the complete suck out would happen around 10GHz, as illustrated in Figure 8. This is the Nyquist frequency for a 20Gbps signal. Extensive simulations must be used to detect and avoid such conditions early in the design process.
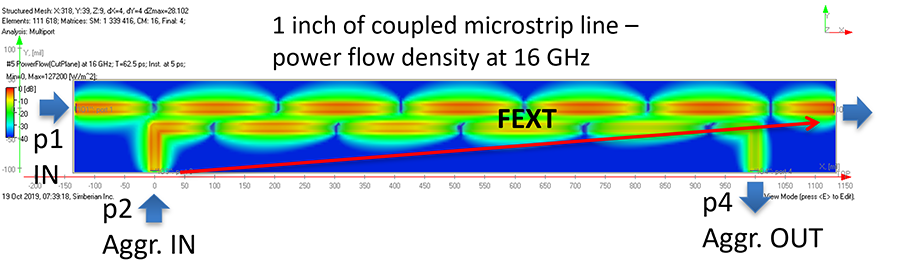
Note that S-parameters of passive interconnects are reciprocal. It means that transmission from port i to port j is always equal to transmission in the opposite direction from port j to port i. This is not a very intuitive property. Applying it to crosstalk, we can state that S41=S14, S21=S12; if the aggressor and the victim are switched, the crosstalk does not change. If the bottom link in Figure 6 has a useful signal, then that link becomes the aggressor for the top link as illustrated in Figure 9. The top link is the aggressor for the bottom link and the bottom link is the aggressor for the top link. The result is the superposition of signals in both links and both links have FEXT.
Up to this point we have investigated the coupling in the frequency domain or for the time-harmonic signals. Digital signals are usually transmitted by pulses, however.1 Let’s take a look at crosstalk in the time domain. To do that, a pulse response can be computed from the S-parameters of the 4-port structure (Figure 10).

Transmission from port p1 to port p3 is characterized by S-parameter S31 on the left graph and corresponding pulse response shown in the middle graph in Figure 10. The bottom link is a potential aggressor in this case – it has leak to port p3 as illustrated with S-parameter S32 in Figure 10. If the bottom link has similar pulse propagating from port p2 to p4, some part of the pulse energy is going to be leaked into port p3 of the top link. Corresponding pulse response for the crosstalk parameter is also shown in the middle graph in Figure 10. If both links have signals propagating in the same direction over the coupled segment, the signals at port p3 will be a superposition of the link pulse response and the crosstalk pulse response as illustrated on the right graph in Figure 10. Because the timing of the pulses at ports p1 and p2 is not synchronized, the crosstalk position is arbitrary with respect to the link pulse. That is what makes the crosstalk difficult to quantify. We can find the worst-case relative timing, but it may never happen.
Let’s return to the near-end crosstalk. S-parameters S21, S12, S34 and S43 describe the near-end crosstalk or NEXT in cases when the signals in the top and bottom links are propagating in the opposite directions as illustrated in Figure 11. The NEXT is frequency-dependent and has nulls at frequencies where the coupled segment is about a multiple of a half of wavelength as illustrated on the left graph in Figure 12. The maxima in NEXT are approximately at frequencies with the wavelength equal to odd multiple of a quarter of wavelength. The near end coupling depends on the length of the coupling section. Though the frequency-domain pattern of the NEXT is considerably different from the FEXT.
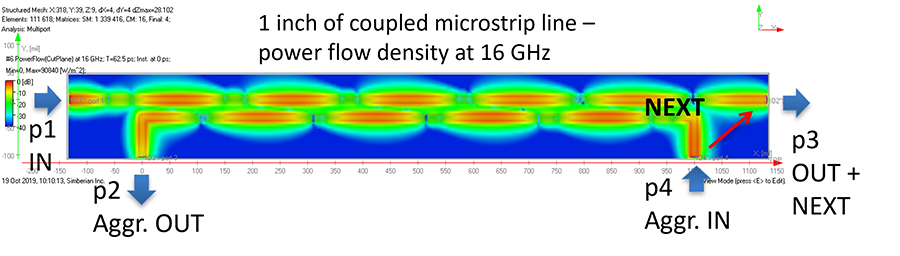
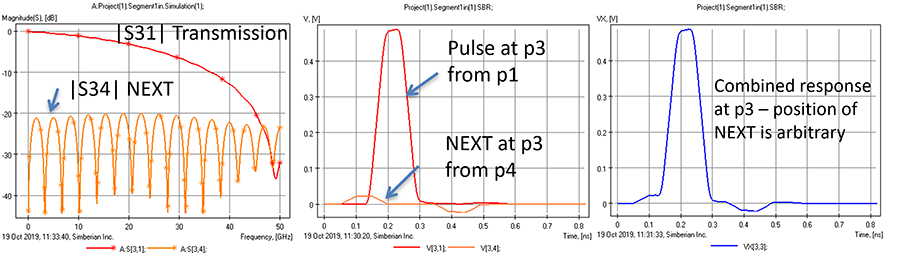
As we can see the level of maxima of NEXT in this case is about -20dB. That gives a relatively small crosstalk pulse response (smaller than FEXT in this case) as shown on the middle graph in Figure 12 together with the pulse transmitted from port p1 to port p3. It comes in two parts: the first appears at the victim port p3 almost immediately, and the second part appears with a delay. There might be no second part for a longer links with substantial attenuation. A superposition of the useful signal and crosstalk at the port p3 is shown on the right graph in Figure 12. As in the case of FEXT, timing of the NEXT with respect to the pulse of the useful signal is also arbitrary. Note that the signal in the victim link may be substantially attenuated at the received end – that means that much smaller values of NEXT can cause failure of the victim receiver. All coupled nets have NEXT. Though, it is important how close to the victim receiver it appears.
Finally, here is how crosstalk in coupled transmission lines can be “explained”. A signal in multi-conductor interconnects propagates as a superposition of multi-conductor line modes – this is a model presentation, but it reveals what happens there and what to expect. For instance, differential signal on the NEXT or FEXT aggressor side becomes a superposition of four waves in coupled two-conductor transmission line segment. Those are the even and odd modes propagation in both directions. The signal cannot remain on just one trace due to the coupling. The waves propagating toward the aggressor side are observed as the NEXT. The waves propagating forward from the aggressor are observed as the useful signal in the aggressor link and as the FEXT at the victim port. If all modes have identical propagation velocity (which never happens in real lossy lines), there will be no FEXT. If the modes are not ideally terminated at both ends, however, the waves forming NEXT are reflected and may appear at the other end as the FEXT. Waves that compose FEXT can be also reflected and become NEXT. To understand different coupling outcomes, a lattice diagram with the transmission line modes superposition can be used, but advanced modeling is an easier way to account for all those reflections.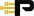
References
1. Y. Shlepnev, “How Interconnects Work: Bandwidth for Modeling and Measurements,” Simberian app. note #2021_09, Nov. 8, 2021.
2. Y. Shlepnev, “How Interconnects Work: Absorption, Dissipation and Dispersion,” Simberian app. note #2021_10, Nov. 26, 2021.
3. Y. Shlepnev, “How Interconnects Work: Impedance and Reflections,” Simberian app. note #2021_11, Dec. 22, 2021.
4. Y. Shlepnev, “How Interconnects Work: Reflections from Discontinuities,” Simberian app. note #2022_01, Jan. 10, 2022.
5. P.J. Pupalaikis, S-parameters for Signal Integrity, Cambridge University Press, 2020.
6. Simbeor Manual: “Multiport Parameters,” https://kb.simberian.com/WebManual_2020/pages/multiport-parameters1.html.
Yuriy Shlepnev is president and founder of Simberian (simberian.com), where he develops Simbeor electromagnetic signal integrity software. He has a master’s in radio engineering from Novosibirsk State Technical University and a Ph.D. in computational electromagnetics from Siberian State University of Telecommunications and Informatics. He was the principal developer of electromagnetic simulator for Eagleware and a leading developer of electromagnetic software for the simulation of signal and power distribution networks at Mentor Graphics. His research has been published in multiple papers and conference proceedings; shlepnev@siberian.com.


