C_pk or P_pk? A Look at Using Both Capability Indices

Summary statistics can be misleading, but in different ways.
by Patrick Valentine, Ph.D.

C_pk and P_pk are numeric capability summaries of process or product characteristics based on common cause variation (due to chance) and assignable cause variation (special cause). Understanding these capability indices and their limitations is critical in pursuing world-class quality, “on target with minimal variation.” C_pk and P_pk indices are reviewed, and details on how to use them synergistically are provided.

Capability indices are numeric summaries that compare the behavior of a process or a product characteristic to customer specifications. Capability indices relate the customer specification limits (voice of the customer) to the natural process limits (voice of the process). Large index values imply that the process can produce parts that meet the customer’s specification limits. Small index values imply the process will likely produce some parts that will not meet the customer’s specification limits.

Process capability is a statistical measure of the inherent process variability of a given characteristic.¹ Capability indices are convenient numeric summaries. These indices reduce complex process information to a single number. Capability indices are unitless values, and can be used to compare the capability of different processes. Most process engineers and quality managers believe capability indices less than 1.00 are unacceptable, and many process engineers and quality managers consider 1.33 a minimum acceptable value for capability indices. Capability indices ≥ 1.50 are generally considered world-class quality, “on target with minimal variation.”

The most common capability indices are C_p | C_pk and P_p | P_pk. C_p measures short-term potential capability, while P_p measures long-term potential performance. C_pk measures short-term actual capability, while P_pk measures long-term actual performance. Potential and actual capability indices are related through k, which measures process centering (the process average).

C_pk and P_pk Indices

C_pk provides an index of the short-term actual capability. Actual capability is based on the process average and standard deviation (common cause variation only). C_pk is calculated as the distance to the nearest specification (voice of the customer) divided by three times the natural process limits (voice of the process; i.e., the standard deviation).

Common cause variation is based only on the variation within the subgroups. This common cause variation standard deviation is known as the within dispersion statistic and is denoted as σ_Within. The C_pk index seriously underestimates the total variation if the between subgroup variation is substantial.¹ Most end-users are concerned with all the variation in the process, regardless of its source. P_pk does not have this inherent underestimation flaw.

P_pk provides an index of the long-term actual performance. Actual performance is based on the process average and standard deviation (common cause and assignable cause variation). P_pk is calculated as the distance to the nearest specification (voice of the customer) divided by three times the natural process limits (voice of the process; i.e., the standard deviation).

Overall variation is comprised of both common cause and assignable cause variation. This common cause and assignable cause variation standard deviation is known as the overall dispersion statistic and is denoted as σ_Overall. The P_pk index estimates the total variation. P_pk accurately tells us “what the customer feels.”

Common and Assignable Cause Variations

Common cause. Causes of variation (due to chance) inherent in a process over time. They affect every outcome of the process and everyone working in the process.² An example of common cause variation is the minor temperature fluctuations of a heated electroless nickel bath due to normal cycling of the heater.

Assignable cause. A name for the source of variation in a process that is not due to chance and, therefore, can be identified and eliminated; also called “special cause.”² An example of assignable cause variation is the major temperature fluctuation of a heated electroless nickel bath due to an operator bringing the tank level to volume by adding cold water.

With variation, the goal then is twofold: 1) continuously strive to reduce common cause variation, and 2) identify and eliminate assignable cause variation. All this effort is put out in pursuit of world-class quality, “on target with minimal variation.”

Visualizing Capability Indices

Consider a car and a garage. The garage represents the specification limits (voice of the customer). The car represents the natural process limits (voice of the process). If the car is wider than the garage, it does not matter if the car is centered; the entire car will not fit in the garage (C_pk | P_pk < 1.0). If the car is the same size as the garage, the car must be centered and remain centered over time to get all of the car in the garage (C_pk | P_pk = 1.0). If the car is narrower than the garage, the car has some wiggle room and can be slightly off-center (C_pk | P_pk > 1.0). With a process that is in control and with little variation, the car can easily park within the garage. FIGURE 1 is a visual image of these capability indices, with a C_pk of ~1.33 depicted.

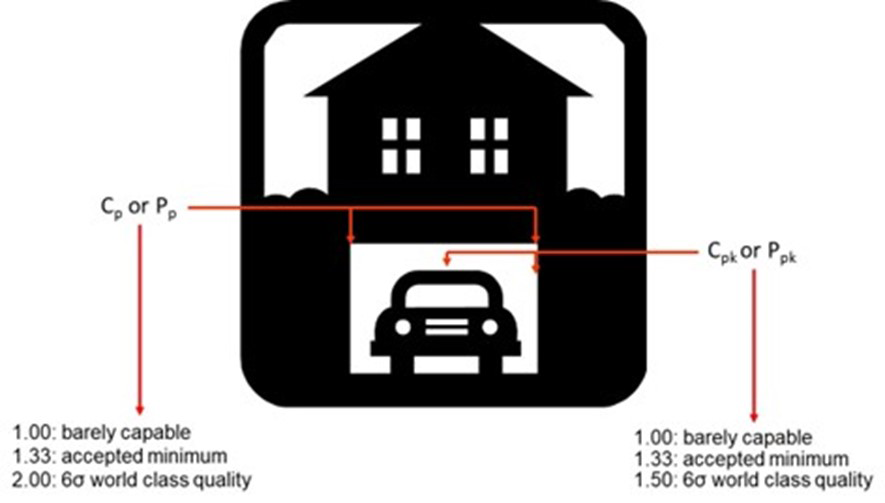
In the car and garage analogy, C_pk | P_pk summarizes the relationship between the size of the car (process), the size of the garage (specification limit), and how far away from the middle of the garage the car is parked. The capability indices values can be considered as the amount the car can drift before hitting the nearest garage wall. Motorola postulated that every process, over many manufacturing cycles, could drift as much as 1.5σ.³ Hence the need for C_pk | P_pk > 1.0. A C_pk | P_pk of 1.33 means there is approximately one-third of the car width between the side of the car and the nearest garage wall. And a C_pk | P_pk of 1.50 means there is approximately half the car width between the side of the car and the nearest garage wall.

Using C_pk and P_pk

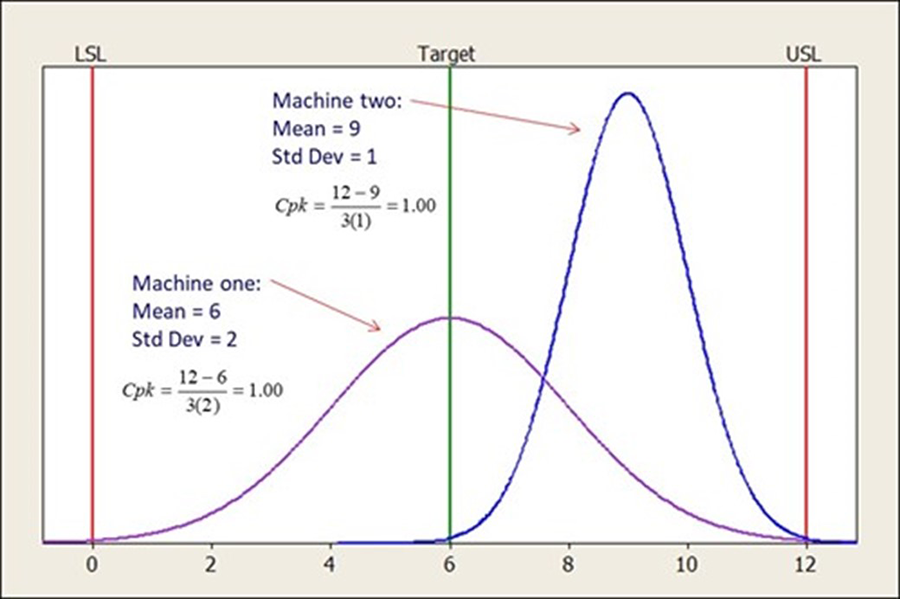
Capability indices are convenient numeric summaries, but summary statistics can be misleading. For example, consider a factory with two machines (one and two) producing the same part. Both machines produce parts that have a C_pk of 1.0. This implies both machine outputs are equal, which may or may not be valid. In this example, it’s not true. Machine one is centered but has a much larger voice of the process (standard deviation). Machine two is not centered but has a much smaller voice of the process (standard deviation); see FIGURE 2. The crucial point is don’t be fooled; always graph your data.

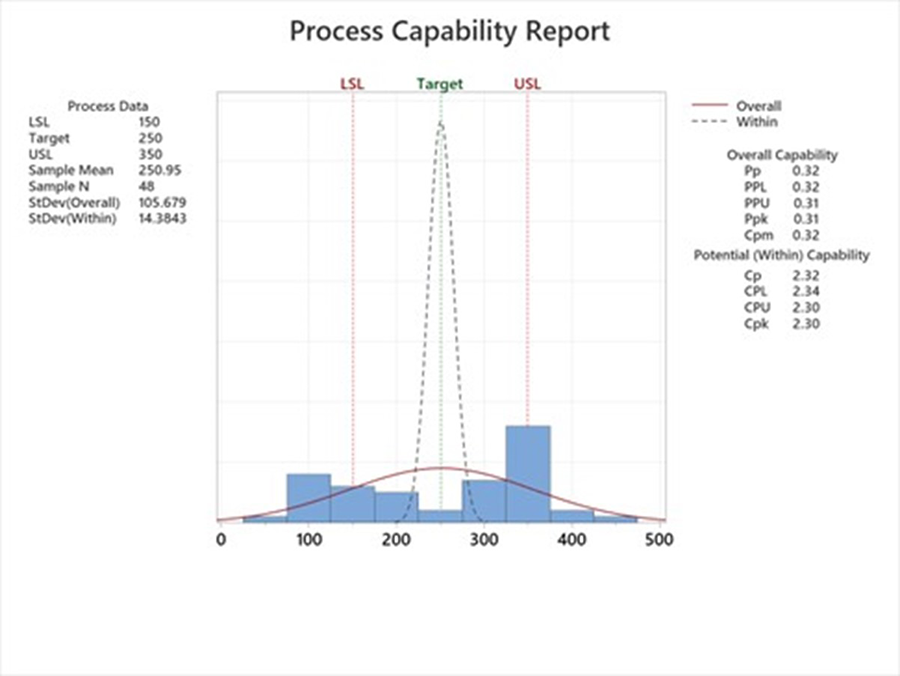
C_pk and P_pk can be used together synergistically. C_pk provides an index of the short-term actual capability based on common cause variation only. P_pk provides an index of the long-term actual performance based on common cause and assignable cause variation. When C_pk ≈ P_pk, the process contains only common cause variation. For example, a process output has a C_pk of 2.30. At face value, one could conclude world-class quality, “on target with minimal variation.” The same process output has a P_pk of 0.31. In this example, C_pk ≠ P_pk, the process contains common cause and assignable cause variation. C_pk seriously underestimates the total variation; see FIGURE 3. In this example, the process engineering team must first identify and eliminate the assignable cause variation, then strive to reduce the common cause variation.

Conclusions

Capability indices are numeric summaries that compare the behavior of a process or a product characteristic to customer specifications. C_pk provides an index of the short-term actual capability but can seriously underestimate the total variation. P_pk provides an index of the long-term actual performance and does not have this inherent underestimation flaw. These summary statistics can be misleading, so always graph your data. In pursuing world-class quality, “on target with minimal variation,” one must identify and eliminate assignable cause variation and continuously strive to reduce common cause variation. The goal is to have C_pk ≈ P_pk, each with a value of 1.50 or greater.

References

1. S. Steiner, et al., Understanding Process Capability Indices, Institute for Improvement of Quality and Performance, The University of Waterloo Department of Statistics and Actuarial Science, 1998.
2. ASQ Glossary of Terms. Retrieved from https://asq.org/quality-resources/quality-glossary.
3. M. Harry and R. Schroeder, Six Sigma: The Breakthrough Management Strategy Revolutionizing the World’s Top Corporations. Currency Publishing, 1999.

Patrick Valentine, Ph.D., is technical and Lean Six Sigma manager at Uyemura USA (uyemura.com); pvalentine@uyemura.com. He holds a doctorate in Quality Systems Management from New England College of Business and ASQ certifications as a Six Sigma Black Belt and Reliability Engineer.